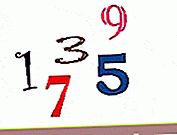визначення натуральних чисел
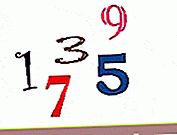Натуральне число називається на номері , який дозволяє вважати елементи множини. 1, 2, 3, 4, 5, 6, 7, 8 ... - натуральні числа .
Слід зазначити, що це були перші набори чисел, які люди використовували для підрахунку предметів.
Цей тип числа необмежений, тобто, коли номер додається один до одного, він поступається місцем іншому номеру.
Два великі способи використання натуральних чисел - це, з одного боку, для позначення розміру кінцевої множини, а з іншого боку, для обліку позиції, яку даний елемент має в рамках упорядкованої послідовності.
Крім того, натуральні числа за велінням групи дозволяють нам ідентифікувати або диференціювати ті елементи, які в ній присутні. Наприклад, у соціальній роботі кожен член філії матиме номер члена, який буде відрізняти його від решти і який дозволить його не плутати з іншим і мати прямий доступ до всіх деталей, притаманних його увазі.
Є ті, хто розглядає 0 як натуральне число, але є й ті, хто цього не робить і відокремлює від цієї групи, теорія множин підтримує його, тоді як теорія чисел виключає.
Натуральні числа можна представити прямолінійно та упорядкувати від найменшого до найбільшого, наприклад, якщо врахувати нуль, вони почнуть зазначатися після цього та праворуч від 0 або 1.
Але натуральні числа належать до множини, яка їх об’єднує, до числа цілих додатних чисел, і це тому, що вони не є ні десятковими, ні дробовими.
Що стосується основних арифметичних операцій , додавання, віднімання, ділення та множення, важливо зазначити, що ці числа є замкненим набором для операцій додавання та множення, оскільки при роботі з ними Ваш результат завжди буде іншим натуральним числом. Наприклад: 3 x 4 = 12/20 + 13 = 33.
Тим часом ця сама ситуація не застосовується до двох інших операцій ділення та віднімання, оскільки результат не буде натуральним числом, наприклад: 7 - 20 = -13 / 4/7 = 0,57.
