визначення теореми
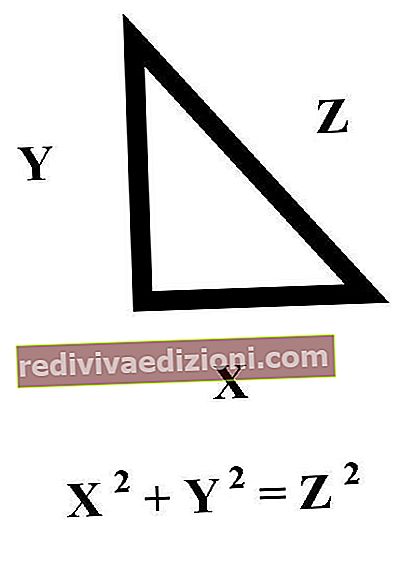Теореми - це потреба та особливе занепокоєння математики, і, говорячи про них, робиться посилання на ті твердження, які можна довести як істинні в логічних рамках .
Як правило, теореми складаються з ряду умов, які можна перерахувати або передбачити заздалегідь, на що їх називають відповідями . Слідом за ними з’явиться висновок або математичне твердження, яке, очевидно, завжди буде справедливим в умовах даної роботи, тобто, перш за все, в інформативному змісті теореми, що буде встановлено, це взаємозв'язок, що існує між гіпотеза і теза або завершення роботи.
Але є щось неминуче для математики, коли певне твердження є вірогідним, щоб стати теоремою, і це полягає в тому, що воно повинно бути досить цікавим всередині і для математичного співтовариства, інакше і, на жаль, це може бути просто девізом, наслідком або просто пропозицією , ніколи не змігши стати теоремою.
І для того, щоб трохи більше прояснити проблему, необхідно також розмежувати згадані вище поняття, щоб, навіть якщо ми не є частиною математичної спільноти, ми могли визнати, коли це теорема, лема наслідок або пропозиція.
Лема - це твердження, так, але це частина довшої теореми. Висновок, зі свого боку, є твердженням, яке слідує за теоремою і, нарешті, судження є результатом, який не пов'язаний з жодною конкретною теоремою.
На початку ми вказали, що теорема - це твердження, яке можна довести лише в логічній структурі, тоді як під логічною структурою ми маємо на увазі набір аксіом або аксіоматичну систему та процес виведення, який дозволить нам вивести теореми з аксіоми та теореми, які вже були виведені раніше.
З іншого боку, скінченну послідовність добре сформованих логічних формул будемо називати доказом цієї теореми.
Хоча і не з особливою увагою, яку математика приділяє теоремам, такі дисципліни, як фізика чи економіка, зазвичай дають твердження, які виводяться з інших і які також називаються теоремами.
